Translate this page into:
Line with attached segment as a model of Helmholtz resonator: Resonant states completeness
⁎Corresponding author. popov1955@gmail.com (I.Y. Popov),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
Quantum graph consisting of a line with attached segment is considered as a simple model of the Helmholtz resonator. Completeness of resonant states in the space of square integrable functions on the segment is proved. Relation between the completeness and the factorization of the characteristic function in Sz.-Nagy model is discussed.
Keywords
Quantum graph
Scattering
Resonance
1 Introduction
The problem of resonances and resonant states attracted great attention starting from famous Lord Rayleigh work (Lord Rayleigh, 1916). But rigorous mathematical description of the problem was given at the end of 20-th century. Particularly, it became clear that resonances are eigenvalues of some dissipative operator (Lax and Phillips, 1967, 1976; Adamyan and Arov, 1965). A few models and asymptotic approaches to the problem were developed on the background of this operator treatment (see, e.g., Hislop and Martinez, 1991; Gadyl’shin, 1997; Popov, 1993; Popov, 1992a,b) and references therein). One of the intriguing question in this problem is: What is a domain which gives one the completeness of the resonant states in ? Our hypothesis is that it is the convex hull of the scatterer. It is not yet proved. There are only some examples of solved particular problems (Shushkov, 1985; Vorobiev and Popov, 2015). There is an interesting relation between the scattering problem and functional model (Sz.-Nagy et al., 2010; Nikol’skii, 2012; Khrushchev et al., 1981; Peller, 2003). More precisely, the completeness is related to the factorization of the scattering matrix characteristic function for the functional model). We use this relation in the present paper. Namely, we consider the simplest, one-dimensional, model of the Helmholtz resonator and investigate the scattering matrix for this quantum graph. This system is, in some sense, close to a waveguide with local perturbation (see, e.g., (Borisov et al., 2001, 2013; Frolov and Popov, 2000; Wulf et al., 2013; Popov and Popova, 1993a,b). The rest of Introduction is devoted to the description of the model.
Let us define the Schrödinger operator on the graph
consisting of three edges
(see Fig. 1) coupled at vertex
.
.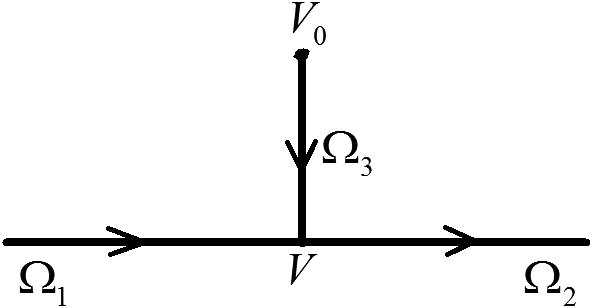
Graph geometry. Arrows show the direction at edges. The origin at
is at vertex
, the origins at
are at vertex
.
Definition. The Schrödinger operator
on
acts as
at each edge
. The operator has the following domain:
Here is the Sobolev space, is the derivative of the solution at the vertex of edge in the outgoing direction from the vertex.
We consider the scattering in the framework of Lax-Phillips approach (Lax and Phillips, 1967, 1976). Let us briefly describe the approach. Consider the Cauchy problem
Outgoing subspace has the following properties:
(a) , ;
(b) ,
(c) .
has the analogous properties (with the natural replacement ).
Subspaces can be chosen as follows:
There is a pair of isometric maps having the following properties: where is the Hardy space.
It is said that gives one the outgoing (incoming) spectral representation of the unitary group . Let Consider a semigroup , is a projector to . Let be the generator of the semigroup . Data which are eigenvectors of are called resonant states. Operator is called the scattering operator. It acts as a multiplication by a matrix-function which is the boundary value at the real axis of analytic matrix-function in the upper half-plane such that for and almost everywhere on the real axis. This analytic matrix-function is called the scattering matrix.
2 Scattering matrix
To describe the scattering matrix and related topics, one can consider the whole set of solutions of the scattering problem having the following form. For the solutions have forms . Here is the transmission coefficient and is the reflection coefficient.
Let us determine an isometric map as a closure of defined on the set of smooth functions in :
Map gives one a spectral representation for the unitary group . The following relations take place. Matrix-function is an inner function in and
As an inner function, can be represented in the form , where is the Blaschke-Potapov product and is a singular inner function (Sz.-Nagy et al., 2010; Nikol’skii, 2012; Khrushchev et al., 1981; Peller, 2003). We are interested in the completeness of the system of resonant states. It is related with the factorization of the scattering matrix.
Theorem 2.2 (Completeness criterion), (Nikol’skii, 2012)
Let be an inner function, , . The following statements are equivalent:
1. Operator is complete;
2. Operator is complete;
3. is a Blaschke–Potapov product.
Here is an auxiliary space (in our case it is ).
As for the case of finite-dimensional (as in our situation), there is simple criterion (for general operator case there is no such criterion) for absence of the singular inner factor (we reformulate the theorem from (Nikol’skii, 2012, p. 99) for the half-plane):
Let . The following statements are equivalent:
1. is a Blaschke-Potapov product;
2.
(3)
One can, immediately, find the scattering matrix for our simple graph (see, e.g., Exner and Seresova, 1994). The coefficients are as follows.
Remark. One can see that if , then the natural property is valid: .
Poles
of the scattering matrix are given by roots
of the equation:
If , then system (9), (10) has no solution in an analytic form. However, the right hand sides of (9), (10) can be simply estimated. Then, the Rouche’s theorem shows that there are only finite number of roots below some line in parallel to the real axis (it is not difficult to obtain the asymptotics of the resonances in , or in ). To prove the completeness, in accordance with Theorem 2.3, we should estimate the corresponding integral in condition (3). Let us describe briefly the procedure of this estimation. There are two reasons of possible breaking of condition (3): infinite length of the integration path after the limiting procedure and singularities appearing time to time at the integration curve when one transforms the curve in accordance with the limiting procedure.
The integration curve
is a circle
.
As for , it is proved that this integral is bounded by a constant which does not depend on . The second integral in (13), , tends to zero if (correspondingly, , ). To prove this statement, we use the information about the resonances (i.e., singularities) positions (particularly, the resonances asymptotics, see above). Consequently, one can perform the limiting procedure in statement 2 of Theorem 2.3. As a result, one comes to the concluding theorem.
The system of resonant states of the Schrödinger operator on the graph is complete in and is not complete in for .
The first part of the theorem has been proved. To prove the second statement, we change the construction slightly. Subspaces can be chosen in another way than in Lemma 1.2:
In this case, a factor appears in the expression for the determinant of the scattering matrix, the space is replaced by . One can see that condition 2 of Theorem 2.3 does not take place, hence, there is a non-trivial singular inner factor. Correspondingly, one can conclude that the system of resonant states is complete in and is not complete in for . QED.
Acknowledgement
This work was partially financially supported by the Government of the Russian Federation (grant 074-U01), by Ministry of Education and Science of the Russian Federation (GOSZADANIE 2014/190, Projects No 14.Z50.31.0031 and No. 1.754.2014/K), by grant MK-5001.2015.1 of the President of the Russian Federation and DFG Grant NE 1439/3-1 (Development of Methods in the Theory of Self-adjoint Extensions), by grant 16-11-10330 of Russian Science Foundation. The authors thanks Referees for useful remarks.
References
- On a class of scattering operators and characteristic operator-functions of contractions. Dokl. Akad. Nauk SSSR.. 1965;160:9-12.
- [Google Scholar]
- Bound states in weakly deformed strips and layers. Ann. Henri Poincare. 2001;2(3):553-572.
- [CrossRef] [Google Scholar]
- Tunneling resonances in systems without a classical trapping. J. Math. Phys.. 2013;54(1):012102.
- [CrossRef] [Google Scholar]
- Resonances for laterally coupled quantum waveguides. J. Math. Phys.. 2000;41(7):4391-4405.
- [Google Scholar]
- Existence and asymptotics of poles with small imaginary part for the Helmholtz resonator. Russ. Math. Surv.. 1997;52(1):1-72.
- [Google Scholar]
- Scattering resonances of Helmholtz resonator. Indiana Univ. Math. J.. 1991;40:767-788.
- [Google Scholar]
- Unconditional bases of exponentials and of reproducing kernels. In: Complex Analysis and Spectral Theory (Leningrad, 1979/1980). In: Lecture Notes in Math.. Vol vol. 864. Berlin New York: Springer-Verlag; 1981. p. :214-335.
- [Google Scholar]
- Scattering Theory. New York: Academic Press; 1967.
- Scattering theory for automorphic functions. Princeton, N. J./Tokyo: Princeton Univ. Press/Univ. of Tokyo Press; 1976.
- Treatise on the Shift Operator: Spectral Function Theory. V. 273. Berlin: Springer Science and Business Media; 2012.
- Hankel Operators and Their Applications. In: Springer Monographs in Mathematics. New York: Springer-Verlag; 2003.
- [Google Scholar]
- Extension theory and localization of resonances for domains of trap type. Math. USSR-Sbornik. 1992;71(1):209-234.
- [CrossRef] [Google Scholar]
- The resonator with narrow slit and the model based on the operator extensions theory. J. Math. Phys.. 1992;33(11):3794-3801.
- [Google Scholar]
- The Helmholtz resonator and the theory of operator extensions in a space with indefinite metric. Russian Acad. Sci. Sb. Math.. 1993;75(2):285-315.
- [Google Scholar]
- Zero-width slit model and resonances in mesoscopic systems. Europhys. Lett.. 1993;24(5):373-377.
- [Google Scholar]
- The extension theory and resonances for a quantum waveguide. Phys. Lett. A. 1993;173:484-488.
- [Google Scholar]
- Structure of resonances for symmetric scatterers. Theor. Math. Phys.. 1985;64:944-949.
- [Google Scholar]
- Harmonic Analysis of Operators on Hilbert Space (second ed.). Berlin: Springer; 2010.
- Model of quantum dot and resonant states for the Helmholtz resonator. J. Phys. Conf. Ser.. 2015;643:012097.
- [Google Scholar]
- A quantitative model for quantum transport in nano-transistors. Nanosystems Phys. Chem. Math.. 2013;4(6):800-809.
- [Google Scholar]






